그래프(Graph)를 탐색하는 방법인 DFS(Depth First Search)와 BFS(Breadth First Search) 대해 알아볼겠습니다.
Graph Search 종류
그래프를 탐색하는 방법
- 깊이 우선 탐색(Depth First Search)
- 너비 우선 탐색(Breadth First Search)
Depth First Search(DFS)
Binary Tree를 검색할때 사용했던 아래 3개가 DFS에 속한다.
- Inorder
- Preorder
- Postorder
- 자식의 자식의 자식...을 계속해서 방문
- 잎 노드를 만나면 다시 올라온다.

Breadth First Search(BFS)
순서대로 레벨별로 자식들을 탐색

DFS, BSF 순서 비교
탐색하는 과정을 순서대로 비교해보며 이해해보겠습니다.

DFS, BSF 과정
과정은 이용하는 자료구조만 바뀌고 동일하다.
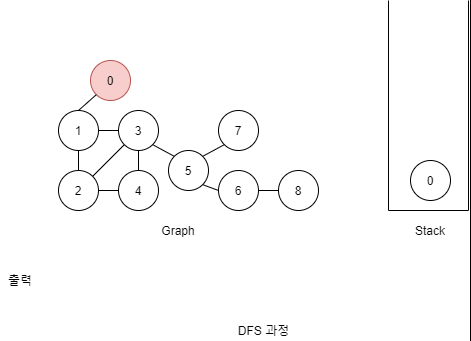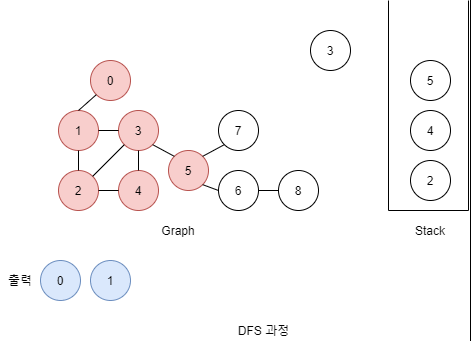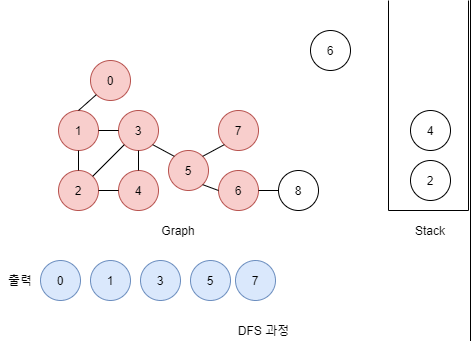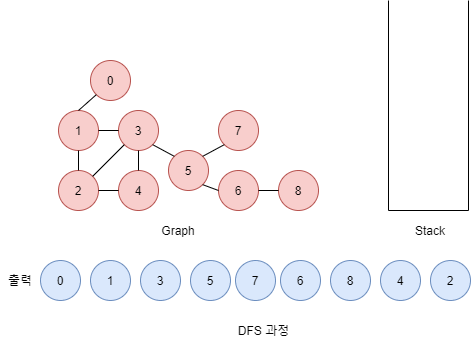
DFS: Stack을 이용
- 빈 스택을 만든다.
- 시작할 노드를 스택에 넣어준다.
- 아래를 반복
- 스택에서 노드 하나를 꺼낸다.
- 꺼낸 노드의 인접한 노드를 전부 스택에 넣는다.
- 꺼냈던 노드는 다시 스택에 넣지 않음
- 인접한 노드가 없다면 다음으로 진행
- 꺼낸 노드는 출력한다.
- 모든 노드를 탐색했다면 종료.
BFS: Queue를 이용
- 빈 큐를 만든다.
- 시작할 노드를 큐에 넣어준다.
- 아래를 반복
- 큐에서 노드 하나를 꺼낸다.
- 꺼낸 노드의 인접한 노드를 전부 큐에 넣는다.
- 꺼냈던 노드는 다시 큐에 넣지 않음
- 인접한 노드가 없다면 다음으로 진행
- 꺼낸 노드는 출력한다.
- 모든 노드를 탐색했다면 종료.

시작점은 항상 0?
위 그래프의 0에서 시작한 DFS, BFS 결과값이다.
- DFS(0) = 0 1 3 5 7 6 8 4 2
- BFS(0) = 0 1 2 3 4 5 6 7 8
그래프는 트리만 있는게 아니기 때문에 시작은 0에서 할 필요는 없다.
예를 들어 3에서 시작해도 순회는 잘 된다.
- DFS(3) = 3 5 7 6 8 4 2 1 0
- BFS(3) = 3 1 2 4 5 0 6 7 8
DFS: Recursion
DFS는 재귀를 통해 보다 쉽게 구현할 수 있다.
방문하면 자신을 출력하고 인접한 노드를 넣어 재귀호출 한다.
재귀는 정방향이기 때문에 자신이 먼저 출력된다.
먼저 입력된 연결 관계에 따라 결과가 달라진다.

DFS, BFS 구현 코드 in Java
import java.util.LinkedList;
import java.util.Stack;
// Queue 강의 참고
class Queue<T> {
// 메소드명 수정
// add => enqueue
// remove => dequeqe
// 생략 ...
}
class Graph {
class Node{
int data;
LinkedList<Node> adjacent;
boolean marked;
Node (int data) {
this.data = data;
this.marked = false;
adjacent = new LinkedList<Node>();
}
}
Node[] nodes;
Graph(int size) {
nodes = new Node[size];
for(int i = 0; i < size; i++) {
// 편의상 인덱스를 값으로 사용
nodes[i] = new Node(i);
}
}
void addEdge(int i1, int i2) {
Node n1 = nodes[i1];
Node n2 = nodes[i2];
if(!n1.adjacent.contains(n2)) {
n1.adjacent.add(n2);
}
if(!n2.adjacent.contains(n1)) {
n2.adjacent.add(n1);
}
}
void dfs() {
dfs(0);
}
void dfs(int index) {
Node root = nodes[index];
Stack<Node> stack = new Stack<Node>();
stack.push(root);
root.marked = true;
while(!stack.isEmpty()) {
Node r = stack.pop();
for(Node n : r.adjacent) {
if(n.marked == false) {
n.marked = true;
stack.push(n);
}
}
visit(r);
}
}
void bfs() {
bfs(0);
}
void bfs(int index) {
Node root = nodes[index];
Queue<Node> queue = new Queue<Node>();
queue.enqueue(root);
root.marked = true;
while(!queue.isEmpty()) {
Node r = queue.dequeue();
for(Node n : r.adjacent) {
if(n.marked == false) {
n.marked = true;
queue.enqueue(n);
}
}
visit(r);
}
}
// 재귀를 이용
void dfsR(Node r) {
if(r == null) return;
r.marked = true;
visit(r);
for(Node n : r.adjacent) {
if(n.marked == false) {
dfsR(n);
}
}
}
void dfsR(int index) {
Node r = nodes[index];
dfsR(r);
}
void dfsR() {
dfsR(0);
}
void visit(Node n) {
System.out.println(n.data + " ");
}
}
/*
------------------
0
/
1 -- 3 7
│ / │ \ /
│ / │ 5
2 -- 4 \
6 - 8
------------------
DFS(0)
0 1 3 5 7 6 8 4 2
BFS(0)
0 1 2 3 4 5 6 7 8
DFS(0) - Recursive
0 1 2 4 3 5 6 8 7
------------------
DFS(3)
3 5 7 6 8 4 2 1 0
BFS(3)
3 1 2 4 5 0 6 7 8
DFS(0) - Recursive
3 1 0 2 4 5 6 8 7
------------------
*/
public class Test {
public static void main(String[] args) {
Graph g = new Graph(9);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(2, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.addEdge(3, 5);
g.addEdge(5, 6);
g.addEdge(5, 7);
g.addEdge(6, 8);
System.out.println("DFS(0) : ");
// g.dfs();
System.out.println("BFS(0) : ");
// g.bfs();
System.out.println("DFS(0) - Recursive : ");
g.dfsR();
}
}링크
아래 강의를 참고하여 작성하였습니다.
'DataStructure' 카테고리의 다른 글
| [HashTable] Hash Table 개념, 구현 (0) | 2021.01.14 |
|---|---|
| [ArrayList] Array List 개념, 구현 (0) | 2021.01.14 |
| [Graph] Graph 개념, 표현 방법 (0) | 2021.01.14 |
| [Tree] Trie Tree 개념 (0) | 2021.01.14 |
| [Tree] Binary Heaps 개념 (0) | 2021.01.14 |